title: Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network
author: Miaomiao
avatar: ‘https://cdn.jsdelivr.net/gh/honjun/cdn@1.6/img/startdash/wangshiwu.jpg‘
authorLink: ‘https://hemiaomiao.github.io/‘
authorAbout: 坚持
categories: 科研
comments: true
tags:
- 论文
- KPI异常检测
photos: ‘https://cdn.jsdelivr.net/gh/HeMiaomiao/cdn/blogImage/202109171644434.jpg‘
date: 2022-04-08 14:35:34
top:
authorDesc:
keywords:
description:
一.标题
Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network
基于随机循环神经网络的多维时间序列异常检测
二.时间
2019年
三.关键字
- Anomaly Detection
- Multivariate Time Series
- Stochastic Model
- Recurrent Neural Network
四.作者
Dan Pei
五.文章来源
SIGKDD:ACM Knowledge Discovery and Data Mining(A类会议)
六.摘要Abstract(介绍作者在做什么 / 知道作者要研究什么)
1.研究背景 / 作者研究这个方向的原因
像服务器、宇宙飞船、发动机这样的工业设备(即实体)是通过多维时间序列进行监控,多维时间序列的异常检测对于保证实体的服务质量非常重要。
注: 多维时间序列 即 多变量时间序列 即 多元时间序列
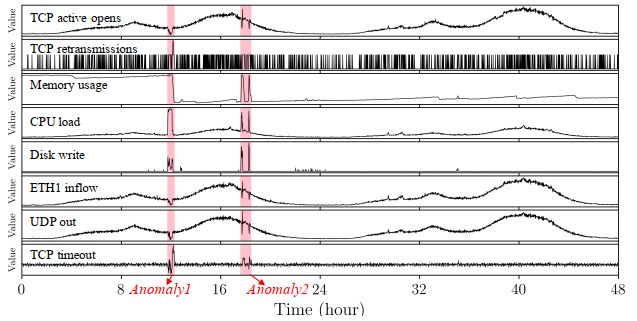
(该图是来自服务器数据集的2天8个指标的多维时间序列片段)
2.研究方向存在的问题 / 作者要解决的问题
因为多维时间序列存在复杂的时间依赖性和随机性,所以多维时间序列的异常检测面临困难。
3.作者解决这个问题的方法
- 提出了模型OmniAnomaly,是针对多维时间序列异常检测的随机循环神经网络,在不同的设备上有很好的鲁棒性
- 模型OmniAnomaly的核心思想:通过随机变量连接(stochastic variable connection)、二维正规化流动(planar normalizing flow)这样的关键技术学习多维时间序列的特征,通过特征重构输入数据,使用重构概率( reconstruction probability)去决定异常,从而捕获多维时间序列的正常模式。
- 模型OmniAnomaly能根据组成的
- 的重构的可能性提供异常的解释。
4.作者模型的效果
在3个实际的数据集上实现了总体0.86的F1-score,超过了前沿的方法0.09,解释的精确度达到了0.89。
5.结论Conclusion
实体水平的异常检测能帮助运维人员及时发现设备的异常,OmniAnomaly模型在不同的设备上有很好的鲁棒性,它的关键技术可以被应用到其它时间序列模型的任务中,另外OmniAnomaly模型根据重构概率可以有效地解释检测到的实体异常。OmniAnomaly模型在三个数据集上超过了前沿的方法,它的优秀表现证明了它是一个鲁棒的模型。
七.引言Introduction
1.研究背景 / 作者为什么要研究这个课题
像服务器、宇宙飞船、机器人辅助系统、发动机这样的工业设备(即实体)是通过多维时间序列进行监控,所以多维时间序列的异常检测对于保证实体的服务质量非常重要。
2.研究现状摘要的第一段扩充 (别人在这个方向上做的相关工作,指出相关工作的局限性 / 目前该课题的研究进行到了哪一步,有什么缺陷)
实体有stochasticity和强的时间依赖性,所以研究应该采取随机性方法和时间独立的模型。但是在多维时间序列的异常检测方面,过去的研究既没有采取确定性的方法,也没有采取随机的方法,而是忽略时间序列的时间依赖性。
3.作者要解决的问题是什么
5.作者提出的模型
作者的核心思想是考虑时间依赖性和随机性,学习潜在的特征去捕获多维时间序列的正常模式。观测值和正常模式之间的差别越大,就更可能是异常。这个想法有两个难题:
考虑多维时间序列的时间依赖性和随机性,怎么去学习潜在特征
- 过去的相关工作:
- 《Sequential neural models with stochastic layers》展现了单独的随机模型是很难去捕获多维时间序列的长期依赖性和概率分布,所以让确定性的RNN的隐藏变量作为随机模型的内部存储器。
- 《A Multimodal Anomaly Detector for Robot-Assisted Feeding Using an LSTM-Based Variational Autoencoder》用基于LSTM的VAE代替前馈神经网络RNN,但是它的随机变量没有时间依赖性。
- 本篇论文的方法:随机变量是输入数据的潜在特征,为了学习输入数据的潜在特征,提出一种随机循环神经网络(stochastic recurrent neural network),对随机变量的时间依赖性进行建模。随机循环神经网络组合了GRU、有随机变量连接和planar Normalizing Flows的VAE。随机变量连接技术是为了在潜在空间对随机变量的时间依赖性进行建模,采用的是线性高斯状态空间模型(Linear Gaussian State Space Model),用来连接随机变量和GRU潜在的变量。planar Normalizing Flows(planar NF)是为了捕获输入数据的分布,它使用一系列可逆的映射去学习潜在随机空间的非高斯后分布。
- 过去的相关工作:
怎么为检测到的实体水平的异常提供解释
- 解释为什么一个观测值被检测成异常
- 本篇论文的方法:因为在实际中运维人员手动检查和解决实体异常的时候,通常会找最偏离历史模式的最重要的几个指标,所以通过一些有最低重构概率的单变量时间序列去解释实体异常。
7.作者的贡献
- OmniAnomaly是第一个多维时间序列异常检测算法,它能解决随机变量的时间依赖性从而学习输入数据的特征
- 提出了第一个基于多维时间序列异常检测算法的异常解释方法
- OmniAnomaly里的四个关键技术:GRU、planar NF、stochastic variable connection、调整的Peaks-Over-Threshold方法在实验里面有很好的效果。
八.相关工作
针对多维时间序列异常检测的方法有以下:
1.监督学习方法
- 论文:
- 《A multimodal execution monitor with anomaly classification for robot-assisted feeding》
- 《 Failure detection in assembly: Force signature analysis》
- 缺点:模型训练需要标签,只能已知的异常类型
2.无监督学习方法
1. 确定性模型(Deterministic model)
论文:
把LSTM用于多维时间序列的异常检测,使用预测错误确定异常
- 《Multivariate industrial time series with cyber-attack simulation: Fault detection using an lstm-based predictive data model》
- 《Detecting Spacecraft Anomalies Using LSTMs and Nonparametric Dynamic Thresholding》
提出了基于LSTM的编码器解码器(Encoder-Decoder),重构正常的时间序列的行为,使用重构错误进行多维时间序列的异常检测
- 《 LSTM-based encoder-decoder for multi-sensor anomaly detection》
缺点:LSTM能解决时间序列的时间依赖性,但是它没有随机变量
2.随机的模型(Stochastic based model)
论文:
提出了DAGMM模型,这个模型融合了自动编码器 (AE)和高斯混合模型(GMM)。使用自动编码器对输入数据进行降维从而得到潜在的特征,使用高斯混合模型估计特征的密度
- 《Deep autoencoding gaussian mixture model for unsupervised anomaly detection》
- 缺点:这个模型是为了多维变量设计的,而不是多维时间序列,忽视了时间序列内在的时间依赖性
表明随机变(stochastic variable)能提高RNN的表现,因为随机变量能捕获时间序列的概率分布
- 《Sequential neural models with stochastic layers》
合并了LSTM和变分自编码器VAE,忽视了随机变量的独立性
- 《A Multimodal Anomaly Detector for Robot-Assisted Feeding Using an LSTM-Based Variational Autoencoder》
3.OmniAnomaly模型和以上两种方法的区别
- OmniAnomaly是组合了GRU和VAE的随机循环神经网络,时间序列的时间依赖性和随机性能被建模。
- OmniAnomaly应用了例如随机变量连接的技术对随机变量之间的时间依赖性进行建模,所以随机变量能更好的代表输入数据。
九.预备知识
1.RNN 循环神经网络
- 参考的论文:《Sequential neural models with stochastic layers》
- 思想:
- 优点:RNN因为采用了确定性的隐藏变量,所以能够代表时间依赖性
- 缺点:简单的RNN不能学习序列的长期依赖性
2.GRU 门控循环单元
- ==本篇论文在OmniAnomaly模型里面采用GRU来捕获时间序列的时间依赖性==
- 参考的论文:《Empirical evaluation of gated recurrent neural networks on sequence modeling》
- 提出的背景:是RNN的变体,通过门控机制解决学习序列的长期依赖性问题
- 思想:
GRU是对LSTM的改进,LSTM有三个门函数:输入门、遗忘门和输出门。GRU有两个门:更新门和重置门。更新门用于控制前一时刻的状态信息被带入到当前状态中的比例,重置门决定了上期信息的遗忘比例。
优点:GRU适合数据集不是非常大的时候用于模型训练,因为GRU比LSTM的参数更少,结构更简单。
- 缺点:
3.LSTM 长短时记忆网络
参考的论文:《Empirical evaluation of gated recurrent neural networks on sequence modeling》
- 提出的背景:是RNN的变体,通过门控机制解决学习序列的长期依赖性问题
- 思想:
- 优点:
- 缺点:
4.变分推断 Variational Inference
- 变分推断的目的是找到一个分布q(z)去逼近没有办法计算的后验分布p(x|z),问题转换为找到一个q(z)令ELBO能够取到最大值
5.VAE 变分自编码器 (Variational Auto-encoders)
- 参考的论文:《Auto-Encoding Variational Bayes》
- 背景:VAE是一个深度贝叶斯定理模型,被成功应用在季节性单变量时间序列的异常检测
- 思想:VAE通过降维把高维的输入$x_t$表示成隐变量$z_t$,然后通过$z_t$重构$x_t$。VAE里面有两个神经网络,分别是推断网络和生成网络。$p_\theta(z_t)$是$z_t$的先验,$x_t$是从后验分布$p_\theta(x_t|z_t)$中采样的,但是后验分布$p_\theta(x_t|z_t)$没有办法计算,在VAE里面通过使用推断网络$q_\Phi(z_t|x_t)$来近似隐变量 Z的后验分布$p_\theta(x_t|z_t)$,推断网络是生成的隐变量z的分布,生成网络是根据隐变量z生成${x}’$的分布。
- VAE和AE的区别:尽管VAE 和自编码器AE 结构类似,区别是VAE 的“编码器”和“解码器” 的输出是变量的概率分布,而不是某种特定的编码
- 在VAE里面使用一种变分推断算法SGVB (随机梯度变分贝叶斯:Stochastic Gradient Variational Bayes)是,通过最大化ELBO (evidence of lower bound )来训练参数$\Phi$和$\theta$,其中$\Phi$是推断网络的参数,$\theta$是生成网络的参数。
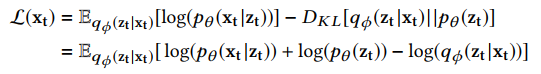
- 蒙特卡罗积分 (Monte Carlo integration)被用来计算上述的期望,$z_t^{(l)}$ ($l$=1,2,……L)是从推断网络$q_\Phi(z_t|x_t)$中采样的。
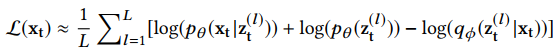
- 在推断网络里面,$q_\Phi(z_t|x_t)$被假设成高斯分布,但是因为$q_\Phi(z_t|x_t)$可能不是高斯分布,所以这个假设可能会使网络过拟合。为了学习非高斯的后验密度$q_\Phi(z_t|x_t)$,论文 (Variational Inference with Normalizing Flows)提出了名叫planar NF的方法。
- planar NF通过使用可逆的映射对后验密度$q_\Phi(z_t|x_t)$进行变换,首先从$q_\Phi(z_t|x_t)$中采样得到$z_t^0$,然后通过一系列可逆的映射得到$z_t^K=f^K(f^{K-1}(…f^1(z_t^0)))$,$f^K(K=1,2…K)$是可逆的映射函数$(f^K(z_t^{K-1})=Z_t^{K-1}+u*tanh(w^Tz_t^{K-1}+b))$(u、w、b是参数),在推断网络里面,使用planar NF的最终输出$z_t^K$作为随机变量$z_t$,即$z_t=z_t^K$。
- 优点:
- 缺点:
6.Planar NF
- 参考的论文:《Variational Inference with Normalizing Flows》
- 提出的背景:是为了学习推理网络里面非高斯的后验密度 $q_ϕ(z_t|x_t)$
- 思想:planar NF通过使用可逆的映射对后验密度$q_\Phi(z_t|x_t)$进行变换,首先从$q_\Phi(z_t|x_t)$中采样得到$z_t^0$,然后通过一系列可逆的映射得到$z_t^K=f^K(f^{K-1}(…f^1(z_t^0)))$,$f^K(K=1,2…K)$是可逆的映射函数$(f^K(z_t^{K-1})=Z_t^{K-1}+u*tanh(w^Tz_t^{K-1}+b))$(u、w、b是参数),在推断网络里面,使用planar NF的最终输出$z_t^K$作为随机变量$z_t$,即$z_t=z_t^K$。
- 优点:
- 缺点:
7.问题描述
- 多维时间序列的定义:$x = {x_1, x_2, …, x_N}$ (N是时间序列的长度)
- 观测值xt是在t时刻M维的向量:$x_t = [x_t^1, x_t^2, …, x_t^M]$
- 多维时间序列x是M行N列的矩阵:$x ∈ R^{M*N}$
- 多维时间序列异常检测的目的是确定观测值$x_t$是不是异常
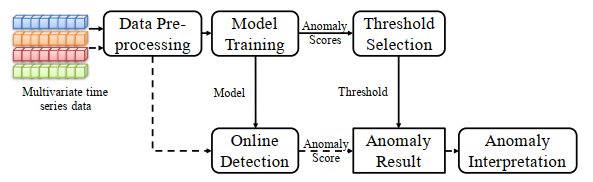
7.OmniAnomaly的总体结构
OmniAnomaly的结构分成两个部分:离线训练和在线检测
离线训练的步骤:(离线训练过程通常定期进行)
- 数据预处理 (data preprocessing)模块:把数据集标准化,然后使用滑动窗口把数据集划分成序列
- 模型训练 (Model Training)模块:经过预处理之后,一个多维时间序列进入模型训练模块,学习一个能捕获多维时间序列的正常模式和输出每个观测值的异常分数的模型
- 阈值选择 (Threshold Selection)模块:得到的异常分数在阈值选择模块使用通过POT方法自动选择一个异常阈值
在线检测的步骤
- 数据预处理 (data preprocessing)模块
- 在线检测 (Online Detection)模块:在线检测模块存储了被训练好的模型,经过预处理之后一个新的观测值进入在线检测模块会得到异常分数
- 异常结果 (Anomaly Result)模块:比较异常分数和阈值选择模块得到的阈值,如果观测值的异常分数比阈值小,那么该观测值就是异常的
- 异常解释 (Anomaly Interpretation)模块:如果观测值是异常的,通过对观测值里面每个维度的估计和贡献排序(ranking the contribution)(例如重构概率)来解释异常
十.作者提出的模型OmniAnomaly的设计
1.OmniAnomaly模型的网络结构
OmniAnomaly的基本思想
- 使用GRU来捕获在x-space里面的多元观测值之间的时间依赖性
- 使用VAE进行特征学习,把观测值映射成随机变量
- 为了对隐空间里面随机变量之间的时间依赖性进行明确地建模,提出了随机变量连接技术SSM (Linear Gaussian State Space Model),==连接随机变量,以及随机变量和GRU隐藏变量的连接==。
- 为了帮助推断网络qnet里面的随机变量捕获输入数据的分布,本篇论文采用了planar NF,planar NF使用一系列可逆的映射来学习隐随机空间里面的非高斯后验分布。
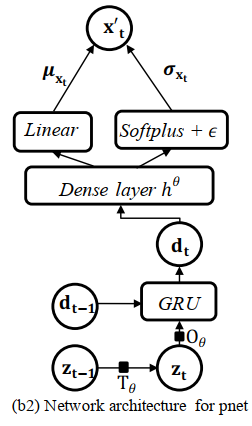
OmniAnomaly的图形模型
OmniAnomaly由推断网络qnet和生成网络pnet组成,OmniAnomaly模型里面的推断网络qnet和生成网络pnet是同时被训练的。
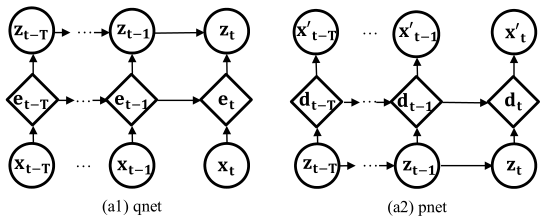
- 节点对应不同的变量,在t时刻,$x_t$是输入的观测值,$x_t^{‘}$是是$x_t$的重构,$e_t$和$d_t$是GRU细胞里面的内存变量,它们是确定性的,$z_t$是z-space的随机变量,边代表变量之间的依赖性。
生成网络pnet:使用隐特征$z_{t-T:t}$去重构输入$x_{t-T:t}$
使用线性高斯状态空间模型 (linear Gaussian SSM) 去连接z-space变量,并且使他们暂时依赖。
- $T_\Theta$是转移矩阵,$O_\Theta$是观测矩阵,$v_t$是转移噪声,$\epsilon _t$是观测噪声
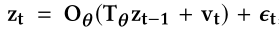
- 在t时刻$z_t$和t-1时刻的变量$d_{t-1}$通过一个GRU细胞去产生一个确定性变量$d_t$
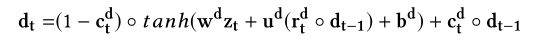
- $r_t^d$是重置门
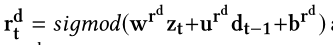
- $c_t^d$是更新门
- $c_{t}^{d}=sigmod(w^{c^{d}}z_{t}+u^{c^{d}}d_{t-1}+b^{c^{d}})$
- 然后$d_t$通过dense layer进一步处理去产生变量${x_t}’$的均值$\mu_{x_t}$和标准差$\sigma_{x_t}$(${x_t}’$是$x_t$的重构)
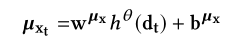
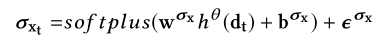
- ${x_{t}}’$是从$\mathbb{N}(\mu_{x_t},\sigma_{x_t}^{2}I)$中采样,从$z_t$中产生
- 如果t时刻有异常,${x_{t}}’$和原始数据$x_{t}$可能会明显不同,所以可以根据$x_{t}$的重构概率去检测异常
推断网络qnet:被优化来接近生成网络pnet,并且获得好的隐特征
- 在t时刻输入的观测值$x_t$和在t-1时刻GRU里面的隐藏变量$e_{t-1}$被送到GRU的细胞从而产生隐藏变量$e_t$,$e_t$是用来捕获$x_t$和之前的x-space观测值之间的长期复杂的时间信息。
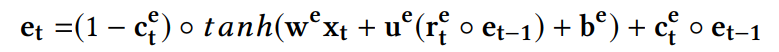
- $r_t^{e}$是重置门,决定怎样和过去的记忆合并一个新的输入。
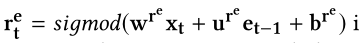
- $c_t^{e}$是更新门,决定过去的记忆需要保存多少。
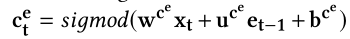
然后$e_t$连接$z_{t-1}$,进入dense layer从而产生随机变量$z_t$的均值$\mu_{z_t}$和标准差$\sigma_{z_t}$。
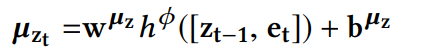
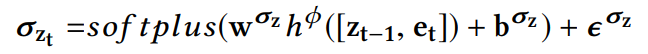
- $h^{\Phi}$表示有ReLU激活函数的dense layer
- $\mu_{z_t}$来自于linear layer
- $\sigma_{z_t}$由soft-plus激活函数和小的$\epsilon$产生,用来阻止数值溢出
- 推断网络qnet的输出$z_t^{0}$是对角高斯,从$\mathbb{N}(\mu_{z_t},\sigma_{z_t}^{2}I)$中采样
- 为了学习非高斯后验分布$q_{\phi}(z_t|x_t)$,使用 planar NF去近似$z_t$,$z_t^{K}$是$z_t^{0}$经过K个二维映射$f^K$变换得到的
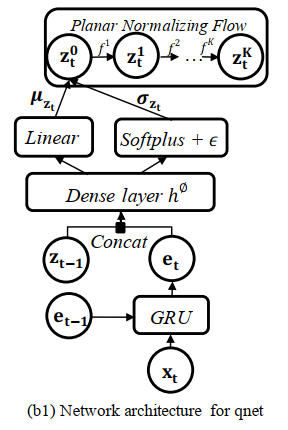
- 在t时刻输入的观测值$x_t$和在t-1时刻GRU里面的隐藏变量$e_{t-1}$被送到GRU的细胞从而产生隐藏变量$e_t$,$e_t$是用来捕获$x_t$和之前的x-space观测值之间的长期复杂的时间信息。
2.离线的模型训练
通过优化ELBO来训练VAE模型,在训练数据集里面每个输入序列数据的长度是T+1,对于第$l$个样本$z_{t-T:t}^{(l)}$ ($1\leq l\leq L$,$L$是样本的长度),损失函数 (loss function) 如下:
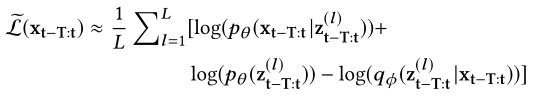
- 第一项$\log (p_{\theta (x_{t-T:t}|z_{t-T:t})})$是负重构误差损失,$x_i$的后验概率$p_{\theta (x_i|z_{t-T:i})}$服从$\mathbb{N}(\mu_{x_i},\sigma_{x_i}^{2}I)$分布
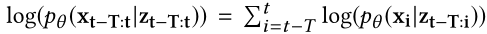
- 第二项和第三项是正则化,也就是KL散度 (Kullback-Leibler loss)
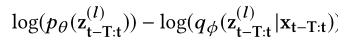
- 第二项$\log (p_{\theta (z_{t-T:t})})=\sum_{i=t-T}^{t}\log (p_{\theta (z_i|z_{i-1})})$,$z_i$是通过用标准多元正态分布初始化Linear Gaussian SSM获得的。
- 第三项$-\log (q_{\phi}(z_{t-T:t}|x_{t-T:t}))=-\sum_{i=t-T}^{t}\log (q_\phi (z_i|z_{i-1},x_{t-T:i}))$,是用来近似推断网络qnet中z空间里面的$z_i$的真实后验分布
- $z_i$即$z_i^{K}$,是通过planar NF变换得到的
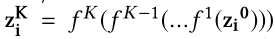
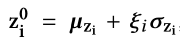
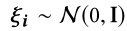
3.在线检测
OmniAnomaly的输入是一个长度为T+1的序列数据,因为采用序列$x_{t-T:t}$作为输入去重构$x_t$,重构能够通过条件概率$\log (p_{\theta (x_{t}|z_{t-T:t})})$进行估计,在模型里面这个重构概率被作为异常分数。$x_t$的异常分数被表示成$S_t$,所以$S_t=\log (p_{\theta (x_{t}|z_{t-T:t})})$。分数越高意味着输入$x_t$被重构的很好,分数越小,则观测值被重构的可能性越小,因此更可能是异常的。如果$x_t$的异常分数$S_t$低于异常阈值,则$x_t$被标记成异常,否则是正常的。
注: $x_{t-T:t}$:是$x_t$和在$x_t$之前的T个连续的观测值
4.自动的阈值选择(离线训练阶段)
- 使用${N}’$个观测值的单变量时间序列,计算出每个观测值的异常分数
- 然后所有的异常分数形成一个单变量时间序列$\left \{ S_{1},S_{2},…,S_{ {N}’ } \right \}$
- 根据极值理论 (EVT:Extreme Value Theory) 的原则设置离线的阈值$th_F$
- 极值理论 EVT:EVT的目标是找到极值定律,极值通常在概率分布的尾部
- 优点:在寻找极值的时候,不假设数据的分布
- Peaks-Over-Threshold (POT):是EVT第二定理
- 基本思想:通过带参数的广义帕累托分布generalized Pareto distribution (GPD)去拟合概率分布的尾部
- ==本篇论文采用POT去学习异常分数的阈值==
- 不像经典的POT专注于分布高端的值,异常位于分布的尾端,所以本篇论文调整GPD函数如下:
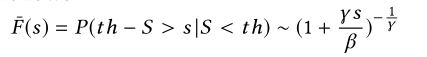
- $th$是异常分数的初始阈值
- $\gamma $是GPD的形状
- $\beta $是GPD的尺度参数
- $S$是$\left \{ S_{1},S_{2},…,S_{ {N}’ } \right \}$的任何值
- 低于阈值$th$的部分被表示为$th − S$,根据经验设置一个低分位数
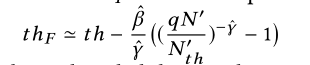
- 通过最大似然估计Maximum Likelihood Estimation(MLE)去估计参数$\hat{\gamma }和\hat{\beta }$
- q是观测$S<th$的概率
- ${N}’$是观测的数量
- ${N_{th}}’$是$S_i$的数量($S_i$<th)
- 对于POT方法,只有两个参数:低分位数(low quantile)和q需要调整,这两个参数能根据经验设置,例如低分位数小于7%,q是$10^{-4}$
- 极值理论 EVT:EVT的目标是找到极值定律,极值通常在概率分布的尾部
5.异常解释
- 目的:异常解释解决方案的目标是用重构概率排名前几位的单变量时间序列去解释检测到的实体异常,所以必须得到每个$x_t^{i}$的重构概率(i是$x_t$的第i个维度)。
- 在OmniAnomaly模型里面,需要计算M维$x_t$的重构概率
- 因为
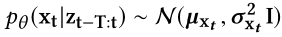
- 所以
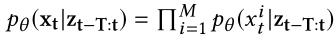
- 所以$x_t$的条件概率被分解成:
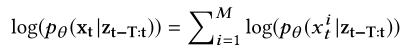
- $p_{\theta }(x_t|z_{t-T:t})\sim \mathbb{N}(\mu _{x_t},\sigma _{x_t}^{2})$
- $S_t^{i}$是$x_t^{i}$的异常分数
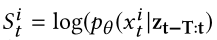
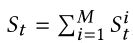
- 对于检测到的异常$x_t$,通过估计$x_t$每个维度的分布(也就是重构概率)来解释异常
- 按照升序对$S_t^{i}$进行排序 ($1\leq i\leq M$),形成列表$AS_T$
- $x_t^{i}$在列表$AS_T$里面的排名越高,则$S_t^{i}$越小,$x_t^{i}$到$x_t$的更高分布
- 列表$AS_T$作为异常解释展现给运维人员,排名高的几个维度能为运维人员理解检测到的实体异常提供足够的线索
十一.实验experiments(作者是怎么通过实验证明自己的模型解决了问题)
1.数据集
在三个数据集上进行实验,证明OmniAnomaly的有效性
- SMD (Server Machine Dataset),
- SMAP (Soil Moisture Active Passive satellite)
- MSL (Mars Science Laboratory rover)
2.评价指标
- Precision
- Recall
- F1-Score (denoted as F1)
F1=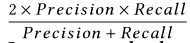
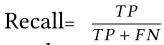
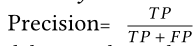
2.实验结果:图和表是怎么证明作者解决了问题
3.实验的步骤
4.每个步骤得出的结论
5.评价指标是什么
6.作者的模型在哪些指标上好,在哪些指标不好
7.作者和什么方法进行了对比,差距是什么