一.标题
Robust and Rapid Clustering of KPIs for Large-Scale Anomaly
用于大规模异常检测的鲁棒快速KPI聚类
二.时间
2018年
三.关键字
四.作者
Zhihan Li, Y oujian Zhao, Rong Liu, Dan Pei
五.文章来源
会议:2018 IEEE/ACM 26th International Symposium on Quality of Service (IWQoS)
六.摘要Abstract(介绍作者在做什么 / 知道作者要研究什么)
1.研究背景
大型互联网公司必须监控KPI和检测异常来保证服务质量
2.作者做这个研究的原因
在上百万的KPI上进行大规模异常检测会因为模型选择的开销、参数调整、模型训练和标签变得很困难
3.作者要解决的问题
聚类算法能把上百万的KPI聚类到少量的簇,然后在每个簇的基础上进行模型选择和训练,但是因为KPI比其它时间序列更长,噪声、异常、相移、振幅的不同会改变KPI的形状,从而误导聚类算法。
4.作者解决这个问题的方法
提出了健壮的和快速的KPI聚类算法ROCKA,模型包括四个步骤:预处理、基线提取、聚类、分配。
5.作者模型的效果
F-score超过0.85,把最好的异常检测算法DONUT的训练时间减少了90%,只有15%的性能损失
6.结论Conclusion(结论是把摘要里面提出的问题用一些实际的结论、数字证明一下)
ROCKA是使用KPI聚类进行大规模KPI异常检测重要的第一步
七.引言Introduction
1.研究方向的背景 / 作者为什么要研究这个课题 / 作者为什么要解决这个问题
大部分异常检测算法(例如Opprentice、EDAGS、DONUT),对于每个KPI都需要一个单独的模型,所以由于模型选择的开销、参数调整、模型训练、异常标签,在数百万KPI上进行大规模异常检测很困难。如果能根据KPI的相似性识别同种类的KPI,然后把它们分成一些簇,可能对于每个簇只需要一个异常检测算法,这样就能减小开销。
2.研究现状摘要的第一段扩充 (别人在这个方向上做的相关工作,指出相关工作的局限性 / 目前该课题的研究进行到了哪一步,有什么缺陷)
时间序列聚类被研究超过20年,但是大部分论都是关注聚类方法和在理想的时间序列数据上进行相似性度量,理想的时间序列通常都是低纬度(通常少于1000个数据点),并且曲线是光滑的,没有异常出现。
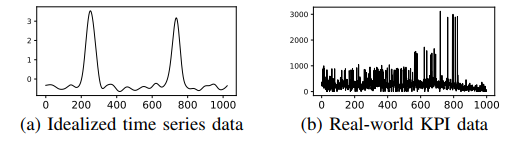
3.作者要解决的问题是什么
KPI聚类面临着两个主要问题:
- 噪声、异常、相移、振幅差异会改变KPI的形状,所以传统的方法没有办法对KPI进行精确地聚类
- 因为为了捕获KPI的模式(例如周期性、季节性),KPI数据的时间跨度从几天到几周,有成千上万个数据点,但是很少有工作研究对有噪声和异常的高维时间序列数据进行聚类
5.作者提出的模型
一种健壮迅速的时间序列聚类算法ROCKA,能对大规模真实KPI数据进行聚类
6.作者的模型是怎么解决问题的(作者的模型在做什么事情)
- 标准化KPI数据,从而排除振幅的差异
- 提取每个KPI的基本形状,称为基线,进一步减少了噪声和异常的影响
- 使用SBD(shape-based distance)作为距离度量,SBD对于相移有健壮性,并且处理高维时间序列数据的计算效率高
- 根据基线的形状相似性使用基于密度的算法进行聚类
- 最后在每个簇里面设置一个代表性的KPI作为质心,新的KPI根据它们到每个簇的质心的距离进行分配
7.作者的贡献点
- 是第一份对KPI这种特殊时间序列数据进行聚类的工作,ROCKA是第一个健壮迅速对长时间序列进行聚类的算法
- ROCKA算法里面有3种技术:基线提取、基于形状相似性的度量、基于密度的聚类方法,三种技术合并在一起获得KPI的基本形状用于聚类
- ROCKA在数据集上超过了最好的聚类算法YADING,F-score超过YADING
- ROCKA把最好的异常检测算法DOUNT的模型训练时间减少了90%,只有15%的性能损失,ROCKA是第一个使用聚类来减少异常检测的训练开销
八.相关工作
1.在作者的研究方向上别人的论文是怎么做的 / 和作者这篇论文相关的工作有哪些
2.之前工作的优缺点是什么
3.作者对之前的哪个工作进行改进
4.之前的工作和作者的联系是什么
5.之前的工作跟自己的区别是什么
九.作者提出的模型
1.存在的问题
真实的KPI和理想的时间序列相比有显著的形状变化:
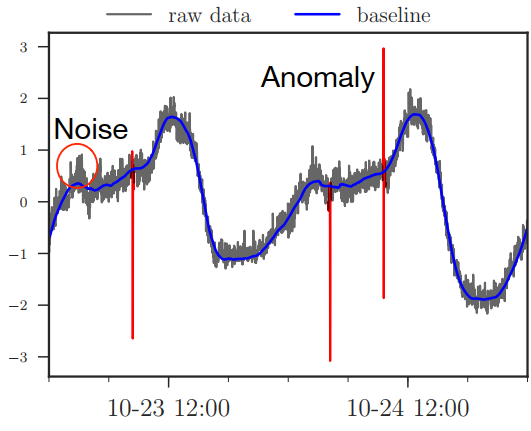
(1) 噪声和异常
- 噪声:是指在一个KPI曲线中期望值周围小的随机波动
- 异常:是指明显的波动,通常超过2个标准差
- 影响:因为噪声和异常能扭曲KPI之间的相似性,所以可能会误导聚类算法
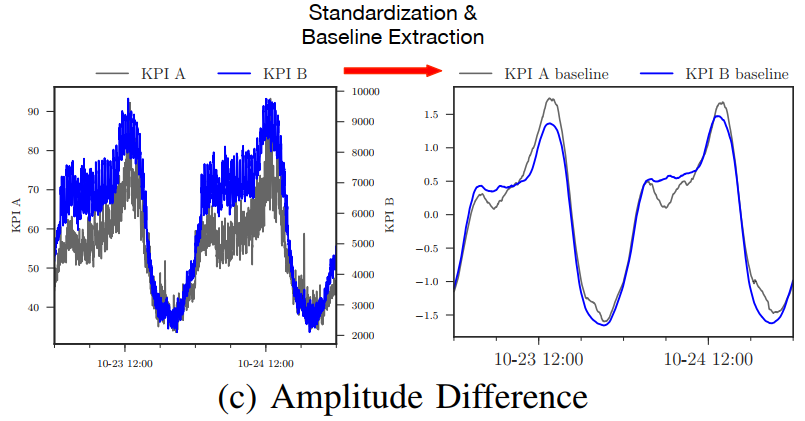
(2) 振幅差异
如果移除KPI的振幅差异,可能有些KPI会有相似的图案,那么这些KPI能被分成一组
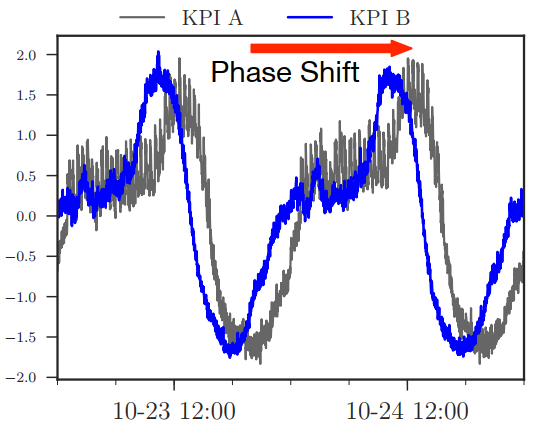
(3) 相移
- 相移:指的是两个KPI之间的全局水平移动
- 影响:相移会让发现相似的KPI变得困难
2.ROCKA模型
(1) ROCKA有四个步骤:
- 预处理:是把原始KPI数据移除幅度差异和标准化数据
- 基线提取:是减少噪声,去除可能是异常的极值,提取KPI的基本形状,称为基线
- 聚类:是在采样的KPI的基线上进行聚类,对噪声和相移是健壮的
- 分配:计算每个簇的质心,把未被标签的KPI根据它们到质心的距离进行分配
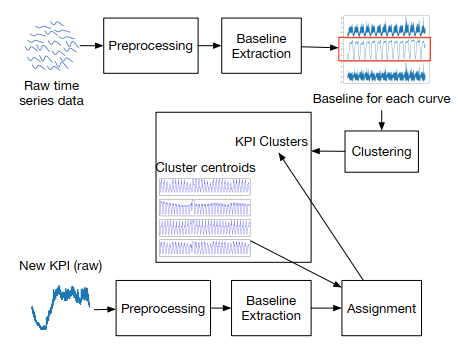
为了对大量KPI进行聚类,提出的聚类模型使用随机采样的KPI的子集,然后分配剩余的KPI到结果簇里。因为即使KPI数量非常大,对于聚类来说只需要小的样本数据集就够了,例如数据集超过9000时间序列,2000个样本就足够聚类。
(2) 预处理
KPI通常都会有缺失值,不过缺失值的比例比较小。
预处理的方法:
- 根据缺失值相邻的数据点使用线性插值的方式填充缺失值
- 标准化:能够移除KPI之间的振幅差异
(3) 基线提取
- 平滑极值:异常是偏离大部分平均值,通常异常点在时间序列数据里面的比例少于5%,所以去除偏离平均值的前5%的数据,然后使用线性插值的方式进行填充
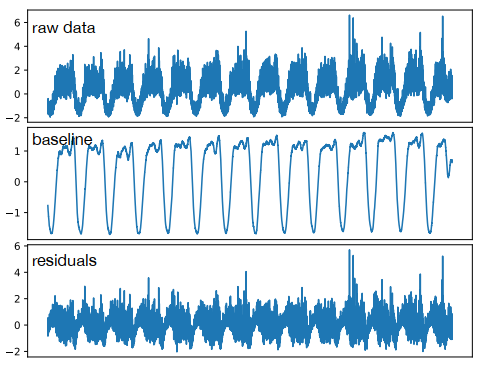
- 提取基线:因为噪声会影响KPI之间的基于形状的相似性,所以需要提取基线代表每个KPI。在KPI上使用滑动窗口移动平均法,把KPI曲线分成基线和残差两部分,残差是原始数据和基线之间的差值。因为残差包含了随机噪声,所以不被用在聚类里面,最后再对基线进行标准化。
(4) 基于密度聚类
根据KPI基线的形状相似性使用基于密度的聚类
1.基于形状的相似性度量
常见的相似性度量:
- Lp norms:简单有效率,但是对噪声、相移、振幅差异敏感
- DTW(Dynamic Time Warping):对相移和其它形状变化具有不变性,但是计算复杂度高,计算两个时间序列的不相似性的复杂度是O(m^2),所以不适合用于高维度的KPI
- cross-correlation:计算两个时间序列的滑动内积(sliding inner-product),适合处理时间序列的相移,使用卷积理论和快速傅里叶变换之后计算复杂度降低到了O(m log(m)),所以适合KPI的相似性度量。
- SBD(shape-based distance):是在cross-correlation基础上提出来的,被用在理想的时间序列
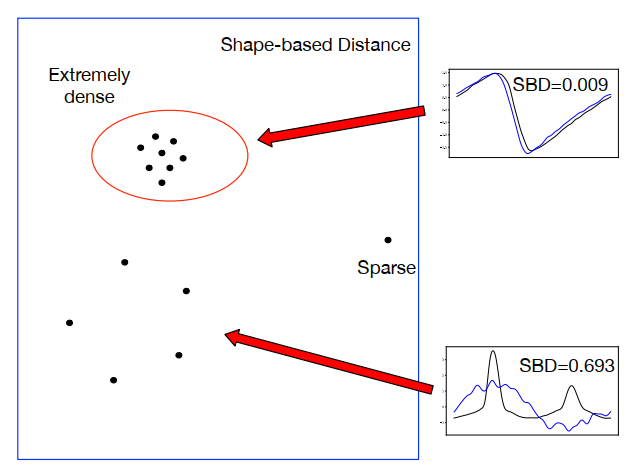
本篇论文使用SBD来度量基线的相似性,SBD值越小意味着形状的相似性越高。基线是标准化的时间序列,没有振幅差异,基线比理想时间序列有更高维度和更多的相移。
2.具有参数估计的基于密度聚类
三种和本篇论文相关的聚类算法:
- 分割法:例如K-Means和K-medoids,簇的数量K需要提前决定
- 特征和基于模型的方法:把时间序列转变成一些特征,把特征放到提前定义的模型里面从而提取更多的数据信息(例如ARIMA),仅仅是复杂的数据集里面使用
- 基于密度的聚类方法:寻找被低密度区域分割的密集的区域从而形成簇(例如DBSCAN)
本篇论文采用DBSCAN作为聚类方法,原因如下:
- KPI很难提前设定簇的数量
- 使用的SBD提供了KPI之间的形状相似性,所以可以利用形状相似性的传递性来扩大簇。例如三个KPIa,b,c,如果a和b在形状上相似,b和c在形状上相似,那么a和c也在形状上相似,所以a和c能分到同一个簇。
3.DBSCAN
- 算法思想:在密集的区域找一些核心,然后通过相似的传递性扩大核心从而形成聚类。一个核心在密度半径(density radius)内至少有minPts个目标(不包括核心本身),一个目标和核心的距离在密度半径内才能形成一个簇,密度半径表示密集区域的密度。
- 步骤:
- 估计密度半径(density radius)的方法:设置minPts=k, $k{dis}$是一个目标和它k个最近的邻居之间的SBD值,曲线平坦的部分的 $k{dis}$值作为候选的密度半径,候选的密度半径的值需要足够的小才能保证一个核心和它的邻居是相似的,如果值大,说明这是一个稀疏的区域,目标之间不相似。一个目标的$k_{dis}$ 值如果大,那这个目标就是一个离群点,它和大多数其它的目标不相似,不应该被聚类到任何簇里面。
寻找候选密度半径:用maxradius表示密度半径的最大值,如果$ k{dis} \leq $ max_d

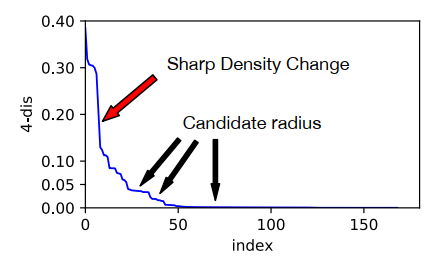
曲线平坦的部分表明在大量的目标的周围密度是连续的,作为候选的密度半径,因为这个部分有大量的核心能去扩大簇
陡峭的部分是明显的密度改变
(5) 分配
十.实验experiments(作者是怎么通过实验证明自己的模型解决了问题)
1.数据集
2.实验结果:图和表是怎么证明作者解决了问题
3.实验的步骤
4.每个步骤得出的结论
5.评价指标是什么
6.作者的模型在哪些指标上好,在哪些指标不好
7.作者和什么方法进行了对比,差距是什么






